Meshing a circle with hex elements in CalculiX
In this article a methd of creating a second order hex mesh for circular cross-sections will be shown.
Circle quadrant
In this method, the circle is basically divided into four quadrants. Therefore a method to generate a quadrant will be shown first.
The code to generate a circle quadrant in the XY plane, extruded in Z is shown below:
## Define the view. rot y rot r 135 rot u 30 ## Dimensions # Radius valu R / 50 1000 # Starting height valu zs / 0 1000 # Thickness valu z / 6 1000 # divisions valu dl 24 ## Geometry pnt pq1 0 0 zs pnt pq2 R 0 zs pnt pq3 0 R zs # Central lines line lq1 pq1 pq2 dl line lq2 pq1 pq3 dl # Arc line lq3 pq2 pq3 pq1 dl surf sq1 blend lq1 lq2 lq3 seta Face1 s sq1 comp Face1 do swep Face1 Face2 tra 0 0 z ## Generate mesh elty all he20r mesh all ## Create image capt Circle quadrant generated by cgx. view elem plus ld all frame zoom 0.7 hcpy png circle-quadrant # Use ImageMagick to trim off the white edges. sys mogrify -trim circle-quadrant.png
The generated image is shown below.
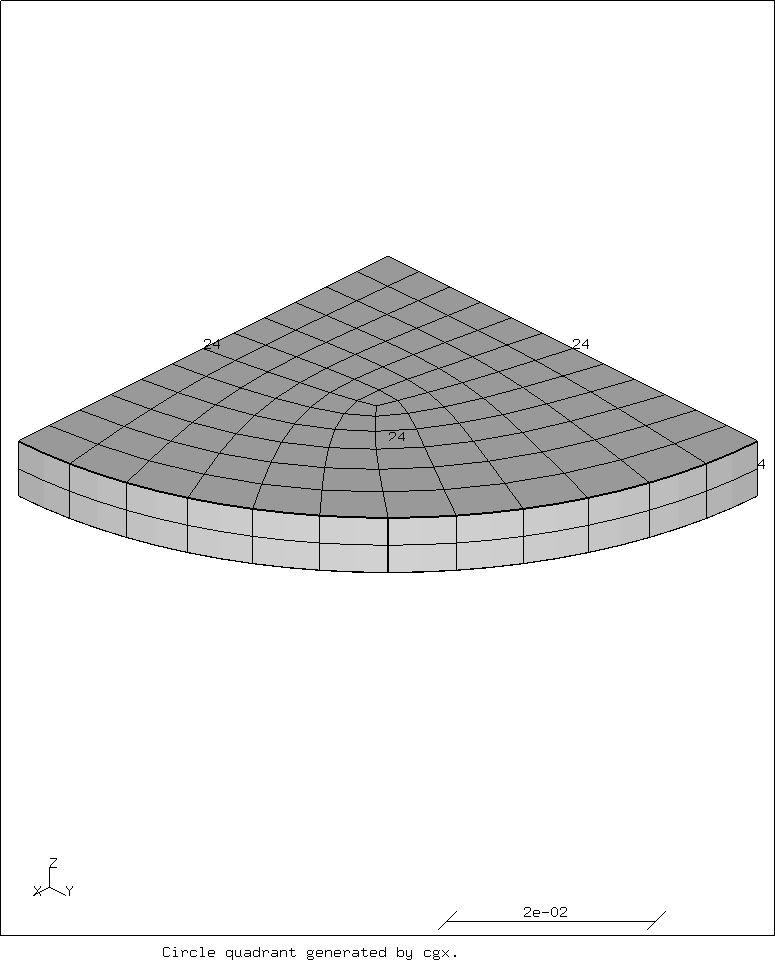
Note how the line divisions are equal for both the lines and the arc. This seems to work the best. Since we are using second order elements, divisions should be a multiple of four. Most numbers divisible by four work for the divisions. Use a higher number for a finer mesh.
Full circle
Instead of one quadrant, four quadrants are now generated:
## Dimension # Radius valu Rc / 50 1000 valu nRc - 0 Rc # Starting height valu zsc / 0 1000 # Thickness valu tc / 6 1000 # divisions valu dlc 24 ## Geometry pnt pc1 0 0 zsc pnt pc2 Rc 0 zsc pnt pc3 0 Rc zsc pnt pc4 nRc 0 zsc pnt pc5 0 nRc zsc line lc1 pc1 pc2 dlc line lc2 pc1 pc3 dlc line lc3 pc2 pc3 pc1 dlc line lc4 pc1 pc4 dlc line lc5 pc3 pc4 pc1 dlc line lc6 pc1 pc5 dlc line lc7 pc4 pc5 pc1 dlc line lc8 pc5 pc2 pc1 dlc surf sc1 blend lc1 lc2 lc3 surf sc2 blend lc2 lc4 lc5 surf sc3 blend lc4 lc6 lc7 surf sc4 blend lc6 lc1 lc8 seta facec1 s sc1 sc2 sc3 sc4 comp facec1 do seto cylc1 swep facec1 facec2 tra 0 0 tc setc ## Show the geometry before extrusion. valu showgeom 1 if showgeom > 0 capt Circle face geometry. plot pa facec1 plus la facec1 plus sa facec1 stop hcpy png circle-geometry sys mogrify -trim circle-geometry.png endif ## Display the mesh valu showmesh 1 if showmesh > 0 capt Circle mesh. elty all he20r mesh all view elem plot e all n view surf stop hcpy png circle-mesh sys mogrify -trim circle-mesh.png endif
This yields the following images. First the geometry.
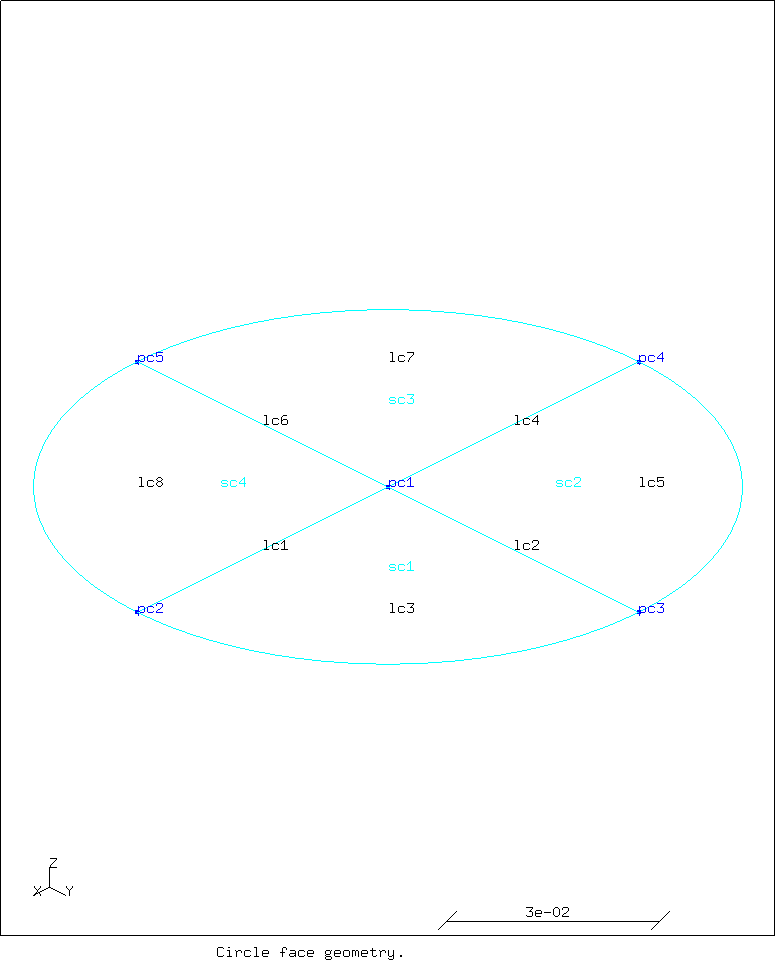
Next the mesh.
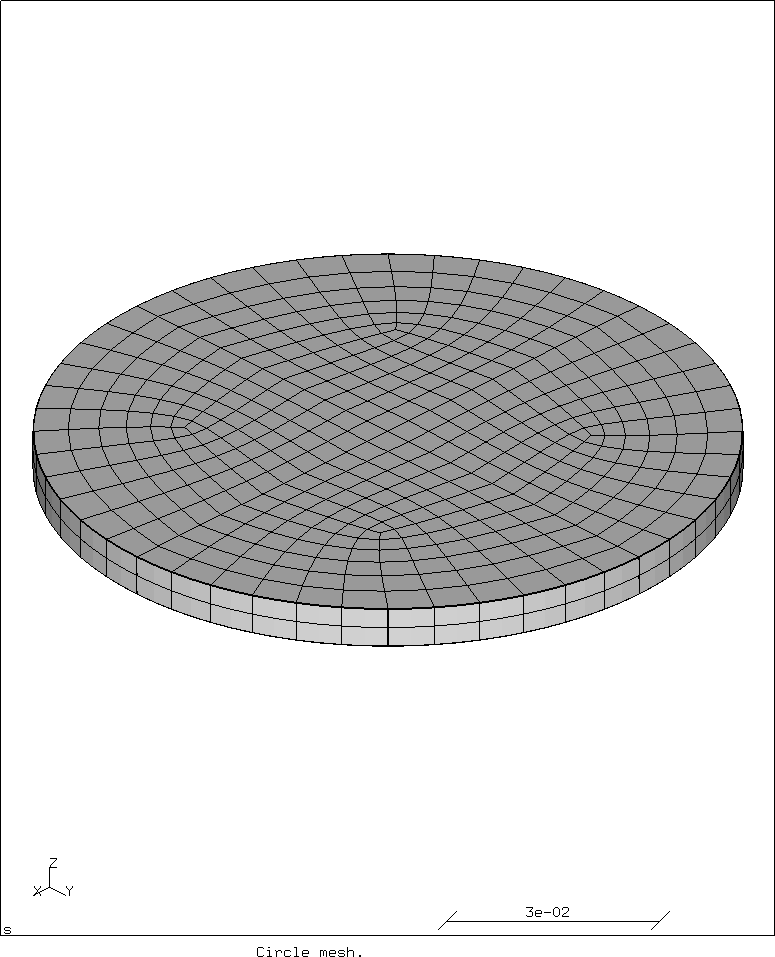
For comments, please send me an e-mail.
Related articles
- Creating a rectangular tube in CalculiX
- Building CalculiX with the PaStiX solver without CUDA
- Element names in Calculix
- FEA based on STEP geometry using gmsh and CalculiX
- Reading CalculiX mesh with Python