Principle

The parametric formulation of an ellipse with major axis a and minor axis b will be used: (x,y) = (a·cos(t), b·sin(t)).

A first approximation could be to divide the range of t equally, in this example over the range 0°—90°.

Code

A Python implementation to generate commands for CalculiX Graphics is shown below.

import math
a, b = 25/1000, 11/1000
center = (0, 30/1000)
segments = 7
j = (math.radians(j*90/segments) for j in range(segments+1))
points = [
    (round(a * math.cos(t) + center[0], 6),
     round(b * math.sin(t) + center[1], 6))
    for t in j
]
indices = []
pi = 1
li = segments # for demonstration purposes
for x, y in points:
    print(f"pnt P{pi} {x:.6f} {y:.6f} 0")
    indices.append(pi)
    pi += 1
print(f"seqa S{li}", end="")
for k in indices[1:-1]:
    print(f" P{k}", end="")
print()
print(f"line L{li} P{indices[0]} P{indices[-1]} S{li} 20")
print("rot z")
print("rot r 180")
print("frame")
print("plot pa all")
print("plus la all")

This results in the following instructions for CalculiX Graphics:

pnt P1 0.025000 0.030000 0
pnt P2 0.024373 0.032448 0
pnt P3 0.022524 0.034773 0
pnt P4 0.019546 0.036858 0
pnt P5 0.015587 0.038600 0
pnt P6 0.010847 0.039911 0
pnt P7 0.005563 0.040724 0
pnt P8 0.000000 0.041000 0
seqa S7 P2 P3 P4 P5 P6 P7
line L7 P1 P8 S7 20
rot z
rot r 180
frame
plot pa all
plus la all

The pnt, seqa and line commands generate the geometry. The remaining commands are to display it.

This procedure yields an acceptable approximation of an ellipse if we choose a high enough number of segments. See the figure below.

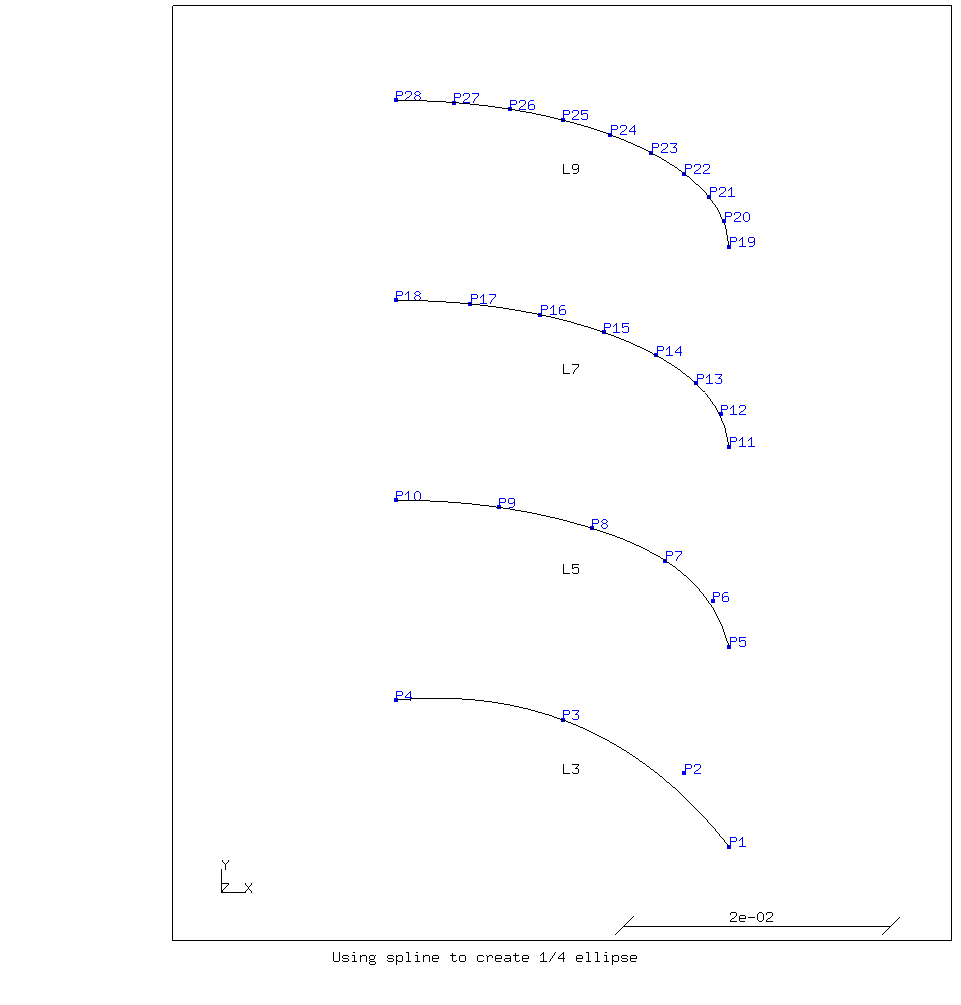
A quarter ellipse approximated by a spline with a different number of nodes.

Five segments or less in a quarter ellipse result in a curve that does not always goes through the control points. Seven to nine segments yield a good result.

It should be noted that a spline in CalculiX Graphics may not have the same start and end point. So a complete ellipse would have to be split up in to at least two splines.

This example is for an elliptical arc with the major axis parallel to the x-axis, and the minor axis parallel to the y-axis. For an arbitrarily oriented elliptical arc, it is necessary to transform the generated points with a rotation matrix before adding the translation with the center coordinates. If the angle φ between the x-axis and the major axis of the ellipse is 20° for example, then the calculation of the points becomes:

j = (math.radians(j*90/segments) for j in range(segments+1))
# Generate points
pairs = (
    (a * math.cos(t), b * math.sin(t))
    for t in j
)
φ = math.radians(20)
cosφ = math.cos(φ)
sinφ = math.sin(φ)
# Transform
points = [
    (x * cosφ - y * sinφ + center[0], x * sinφ + y * cosφ + center[1])
    for x, y in pairs
]

In my dxf2fbd program, I use this technique to convert ELLIPSE entities. See the linked source code for details.